Adap
Purpose:
- calculation of coefficients of expansion of a function specified by a set of samples into a Fourier series in classical orthogonal polynomials and functions
- edition of data using orthogonal expansions
- calculation of derivatives, definite/indefinite integrals
- trigonometric Fourier polynomials
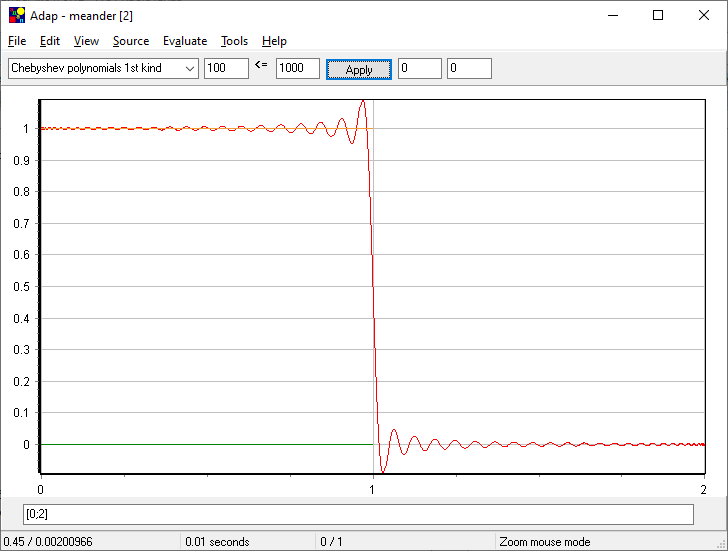
- algebraic polynomials of Legendre, Chebyshev of the first and second kind, Jacobi
- orthogonal functions of Sonin-Laguerre, Hermite
- Bernstein polynomials
- linear interpolation
- Gaussian quadrature formulas
- Fejer summation method
- Clenshaw recurrence formula
- algebra of orthogonal series
- nodes and weights of Gaussian quadrature formulas (output only)
- expansion coefficients
- function value table
- - selection of basis functions
- - number of terms of the orthogonal series
- - number of nodes of the Gaussian quadrature formula function
- - application button
- - parameter alpha of the Sonin-Laguerre and Jacobi bases
- - scale factor for the Sonin-Laguerre and Hermite bases or the beta parameter of the Jacobi basis
- - approximation interval
- - approximation error (quadratic/infinite norm)
- - operation execution time
- - area (signal without trend/approximation)
- - status of the left and right mouse buttons (zooming and dragging/entering left and right interval boundaries)
 SBARS.IMPB.RU
en |
SBARS.IMPB.RU
en |